Тьюринг-полнота CSS
Если загуглить что-то вроде "Является ли CSS полным по Тьюрингу", первыми ответами в поисковом запросе будут реализации Правила 110 - одномерного клеточного автомата с доказанной полнотой по Тьюрингу. Пример другого известного клеточного автомата - игра "Жизнь". Он тоже полон по Тьюрингу, но излишне сложен в силу двухмерности.
Первые 16 шагов правила 110, Стартовая позиция - 1 клетка в центре. Источник
Что уже есть
Реализаций можно найти множество: на Stackoverflow, на Github, на сайтах других людей. Однако все, что я нашёл, имеют существенное "но" - HTML + CSS страничка во всех этих примерах требует от пользователя прокликивать подсвеченные ячейки. Данное действие тоже автоматизируется, например в этом примере выше достаточно многократно нажимать Tab и пробел, однако у меня возник вопрос: можно ли минимизировать ввод от пользователя, сохранив функциональность?
Чем можно воспользоваться
С 2016 года большинство современных браузеров начали поддерживать
"пользовательские свойства", или, проще говоря, переменные в CSS. Это может звучать как
ультимативное решение, однако стоит учесть их ограничения: в CSS нет массивов, нет
логического типа данных, есть всего 4 базовые арифметические операции (стандартные
+, -, * и /), и, что самое главное - куда сложнее организовать подобие циклов.
Любой CSS с рекурсивным вычислением переменных в одной области видимости автоматически перестаёт вычислять их значения, так что придётся хитрить. Первая идея - использовать рекурсивно вложенные блоки. Так как CSS - это каскадные таблицы стилей, значение переменной, вычисленной в конкретном блоке, доступно только в нём и его потомках. Но его можно переопределить в любом подблоке, как в более локальной области видимости, по аналогии с обычными языками программирования.
Саму логику вычислений можно организовать, используя числа 1 и 0 и логические операторы из арифметических операций. Я нашёл целую статью про то как их можно собрать и применить на практике для 3D на чистом CSS.
Формула правила 110 есть на русской википедии (на английской нет):
(p, q, r) ↦ (q AND (NOT p)) OR (q XOR r).
Простейший способ записать NOT арифметически - (1 - x), AND - (x * y). Этих
двух операторов уже достаточно для функционально полной системы, и из них легко
выводится OR по закону де Моргана - (1 - (1 - x) * (1 - y)),
и XOR - (x + y - 2 * x * y).
Итоговая формула в арифметической записи:
1
2
3
4
5
1 - (
1 - (q * (1 - p))
) * (
1 - (q + r - 2 * q * r)
)
Первая реализация
Ввод данных работает так же, как и в других примерах - на чекбоксах в первой строке.
Во избежание циклических формул каждая последующая строка находится на 2 уровня
вложенности глубже, чем предыдущая: на первом значение из переменных v дублируется в
b, а на втором значение более локальных v вычисляется по формуле из b. Итоговое
количество переменных - по две на столбец, с нумерацией с нуля: --v0 и --b0, --v1 и
--b1 и так далее.
Вывод данных осуществляется при помощи классов ci, которые меняют цвет по формуле
hsl(0, 0%, calc(100% - 100% * var(--vi))), становясь чёрными, если соответствующая
переменная --vi равняется единице.
После небольшой доработки декоративной части пример заработал... первые 4 шага.
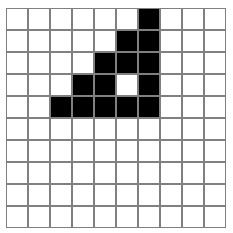Строка ввода, вычисленные 4 шага и пустые ряды внизу.
Оптимизация
Вполне ожидаемо в браузерах есть существенные ограничения, которые останавливают вычисление формулы на четвёртой итерации. Из интересного, в Firefox эти ограничения куда меньше - вычисляется сразу 6 шагов, что всё ещё мало, но больше, чем в Chromium.
Опытным путём выяснилось, что браузеру не важно количество операторов в формуле, но важно
количество использованных в формуле упоминаний переменных - чем меньше ссылок на
предыдущий ряд, тем больше строк вычисляется. В формуле в Википедии в записи с логическими
операторами переменных всего 4, однако оператор XOR в аналитическом виде имеет в себе по
2 записи входных переменных, итого 6. У меня получилось сократить её до 5:
(p, q, r) ↦ (q OR r) AND NOT (p AND q AND r)
с соответствующей куда более короткой аналитической записью:
(1 - (1 - q) * (1 - r)) * (1 - p * q * r).
Страничка c новой формулой, её исходник. Оптимизация формулы добавляет по ещё одному шагу как в Chromium, так и в Firefox, что позволяет в полной мере раскрыть потенциал правила и вывести амогуса.
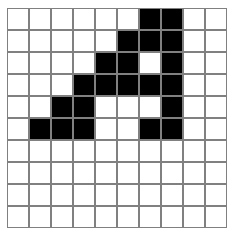sus.
Любопытному читателю предлагается (в интересах автора, конечно же) попробовать оптимизировать формулу ещё сильнее или доказать невозможность выразить её записью менее чем с 5 переменными.
Второй идеей для оптимизации было попробовать убрать промежуточные переменные --bi, для
чего я убрал вложенность и сделал отдельную переменную для каждой ячейки, но как оказалось
это ни на что не влияет - как не ухудшает ситуацию из-за 100 отдельных переменных в CSS
вместо 20, так и не улучшает из-за отсутствия дублирования значений и меньшей вложенности.
В любом случае посмотреть на попытку можно тут, исходник.
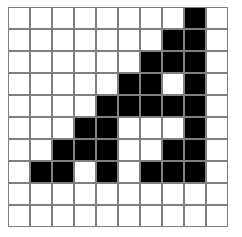Последняя версия в Firefox
Можно ли это применить?
В виде машин Тьюринга - вряд ли, но на одном CSS можно делать очень даже интерактивные игры, я нашёл целый сборник таких. Из самого примечательного в ней есть полностью рабочий сапёр, хоть и с неудобным управлением, и "платформер" с персонажем в виде мышки.
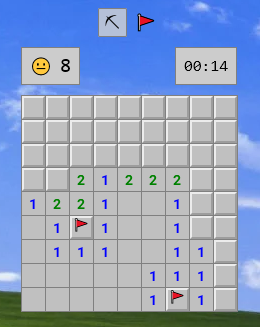
Не пригодившееся
Помимо статьи про логические операторы, я нашёл и статью про более сложные
математические функции (для реализации 3D): модуль, сигнум, округление и остаток
от деления, но все они построены на экспериментальном правиле @property, которое пока
что поддерживается не всеми браузерами.